Darcy’s law, a fundamental principle in fluid dynamics, has revolutionized our understanding of fluid flow through porous materials, like groundwater movement in aquifers. Developed by Henry Darcy, this law finds widespread applications in various fields, including petroleum engineering and environmental sciences. Read on to know the core principles of Darcy’s law, its formulas regarding the conditions and application, and its practical relevance for real-world scenarios.
What Is Darcy’s Law?
Darcy’s law is a principle formulated by Henry Darcy that explains the movement of fluids through porous materials, such as water flow through sand beds or rocks. It serves as a cornerstone in the field of hydrogeology, a branch of earth sciences.
Darcy’s law is established on the principle that the flow between two points is directly proportional to the pressure difference, distance, and flow connectivity within rocks. The evaluation of this connectivity is referred to as permeability.
How Is Darcy’s Law Application?
Darcy’s law finds practical use in various scenarios, including groundwater flow through aquifers. It is an essential component of the groundwater flow equation, crucial in hydrogeology. Additionally, Darcy’s law is employed to understand the flows of oil, gas, and water in petroleum reservoirs.
The movement of liquids within rocks is influenced by the rock’s permeability, which must be determined both horizontally and vertically. For example, shale exhibits lower vertical permeability, making it challenging for liquids to flow up and down through shale beds but easier for lateral flow.
How Is Darcy’s Law Application in Petroleum Engineering?
In petroleum engineering, another form of Darcy’s law is extensively used to determine flow through permeable media. This derivation is often applied to one-dimensional, homogeneous rock formations with a single fluid phase and constant fluid viscosity.
Oil reservoirs typically have a water zone below the oil leg and sometimes a gas cap above the oil leg. As reservoir pressure decreases during oil production, water flows into the oil zone from below, and gas enters from above (if a gas cap exists). This leads to simultaneous flow and immiscible mixing of all fluid phases in the oil zone.
To optimize oil production, operators may inject water and/or gas. In the petroleum industry, a generalized Darcy equation for multiphase flow, developed by Muskat et al., is widely used. Despite its broad adoption, it’s often referred to as Darcy’s law for multiphase flow or the generalized Darcy equation (or law) due to the strong association of Darcy’s name with flow in porous media.
When discussing the multiphase equation by Muskat et al., it is commonly referred to as Darcy’s equation (or law) or simply the flow equation. Multiphase flow in oil and gas reservoirs is a complex topic, and one of many articles covering this subject is Darcy’s law for multiphase flow.
What Is Darcy’s Law Reference?
Darcy’s law, an essential principle in fluid dynamics, explains fluid flow through porous materials like groundwater movement. It was introduced by Henry Darcy and holds great importance in hydrogeology, studying Earth’s water resources.
Since its inception, Darcy’s law has found applications in diverse fields, including petroleum engineering, environmental sciences, and civil engineering. Over time, experts have refined and adapted its principles, leading to specialized formulations for specific situations. One such adaptation, the generalized Darcy equation, considers multiphase flows, making it valuable for analyzing fluid dynamics in oil and gas reservoirs.
Researchers and practitioners continually build upon Darcy’s work, developing advanced models and simulations to enhance our understanding and management of subsurface fluid flow. As a widely recognized concept in fluid mechanics, Darcy’s law serves as a fundamental reference for those involved in fluid dynamics, porous media, and groundwater studies.
What Is The Main Assumption of Darcy’s Law?
Darcy’s law, refined by Morris Muskat, explains fluid flow in a uniformly permeable medium without gravitational forces. It shows a simple relationship between the instantaneous flux (q) through the porous medium, the medium’s permeability (k), the fluid’s dynamic viscosity (μ), and the pressure drop (Δp) over a specific distance (L). The units of Q are m³/s, A is m², and q is m/s.
1. Darcy’s Law General Formula
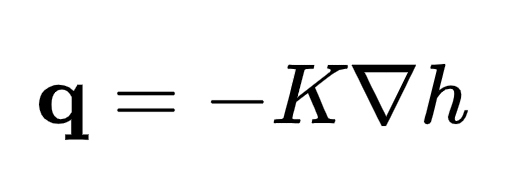At a specific point in the medium, q represents the volume flux vector of the fluid, h signifies the total hydraulic head, and K represents the hydraulic conductivity tensor. In many cases, the hydraulic conductivity can be estimated as a scalar.
2. Darcy’s Law in Single-Phase Permeability
Below formula represents single-phase fluid flow and serves as the fundamental equation for absolute permeability (single-phase permeability).
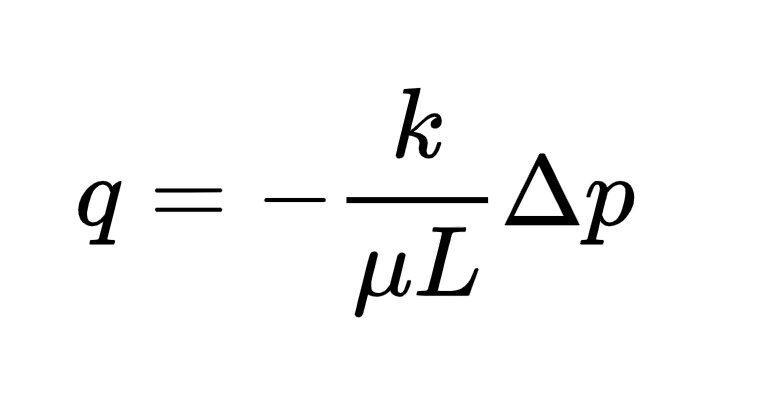
3. Darcy’s Law in Absolute Permeability
Several suggestions have been made regarding the constitutive equation for absolute permeability, and the most well-known among them is likely the Kozeny equation (also referred to as Kozeny-Carman equation).
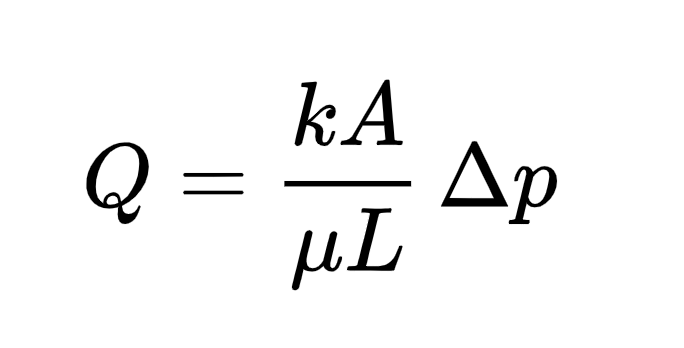
Where Q (measured in volume per time, e.g., m3/s) represents the total discharge. This consideration involves the relationship with static fluid pressure, known as Stevin’s law.
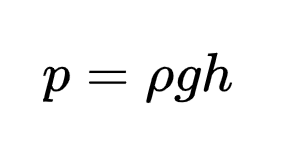Through analysis, one can derive the representation:
Incorporating the kinematic viscosity (represented by ν), we obtain the corresponding hydraulic conductivity as follows:
Please take note that the quantity q or Q/A, commonly known as the Darcy flux or Darcy velocity, does not represent the fluid’s actual velocity within the pores. The flow velocity (u) is associated with the flux (q) through the porosity (φ) and can be expressed as follows:
Darcy’s law presents a straightforward mathematical statement that encapsulates several essential characteristics of groundwater flow in aquifers. These include:
- Under hydrostatic conditions (no pressure gradient over a distance), no flow occurs.
- When a pressure gradient exists, flow moves from high pressure to low pressure (opposite the direction of the increasing gradient, as indicated by the negative sign in Darcy’s law).
- A higher pressure gradient (within the same formation material) leads to a greater discharge rate.
- The discharge rate of the fluid can vary when flowing through different formation materials or even in different directions within the same material, even if the same pressure gradient exists in both cases.
3. Darcy’s Law for Short-Time Scales
For extremely brief time intervals, a time derivative of flux can be incorporated into Darcy’s law. This modification allows for valid solutions when dealing with very small time scales, a concept known as the modified form of Fourier’s law in heat transfer.
The presence of τ, a significantly small time constant, causes this equation to revert to the standard form of Darcy’s law during “normal” times, typically greater than nanoseconds.
What Are The Limitations of Darcy’s Law?
Darcy’s law, while widely useful, has certain limitations to consider in specific situations:
Heterogeneous Media
Darcy’s law assumes uniform and isotropic porous media, which does not take into account real-world variations in permeability.
Low Flow Velocities
It is best applied to low flow rates and may be less accurate in turbulent conditions.
Single-Phase Flow
Darcy’s law is primarily suitable for single-phase fluid flow, making it less ideal for analyzing multiphase flow scenarios.
Compressibility and Capillary Effects
The law does not consider fluid compressibility and capillary forces, which can be significant in certain cases.
No Thermal Considerations
Darcy’s law solely focuses on fluid flow and neglects thermal effects relevant in heat transfer applications.
Unsaturated Flow
The law is not directly applicable to unsaturated flow conditions, where the water content in the pores is not at its maximum capacity.
Macroscopic Description
It offers a macroscopic view, potentially missing out on microscale interactions in nanoporous media.
Despite limitations, Darcy’s law remains valuable, but its use requires careful consideration for accurate results. Understanding Darcy’s law is crucial for engineers in the oil and gas industry as it provides a fundamental basis for comprehending how fluids move within underground reservoirs.
By grasping Darcy’s law, you can measure and predict how fluids such as oil, gas, or water will flow through porous materials and reservoir rocks. This knowledge aids in calculating fluid flow rates and pressures within the reservoir, which is essential for assessing the production potential of oil and gas and designing effective production wells.
PetroSync offers a well completion and workover training that covers Darcy’s law and its practical applications in the oil and gas industry. Our well completion and workover course equips you with hands-on experience and valuable knowledge to optimize production and troubleshoot fluid flow challenges in reservoirs. Whether experienced or new to the field, this training synchronizes your’ skills with industry best practices.
Credit header image: freepik.com
Reserve Your Training Seat!
Enhance your skills with the latest industry knowledge. Kickstart your career growth with PetroSync training today!
SEO specialist by day, fact-checker by night. An avid reader and content writer dedicated to delivering accurate and engaging articles through research and credible sources.
